カルマンフィルタについて
この記事は東京大学航空宇宙工学科/専攻 Advent Calendar2017の七日目の記事として書かれています。
最近流行りの自動運転とか気象予測なんかにも使われていて古くはアポロ計画にも用いられたことで有名なカルマンフィルタについてまとめてみました!・・・と言いたいところですが、半分くらい自分向けの備忘録の様相を呈しているので全然まとまっていません。あしからず。
はじめに
卒論も終わって久々にtwitterを眺めていたら同期の某うさぎさんがなにやら面白いことを初めていたので興味本位で応じてみました。
とは言ってもブログなんて一切やったことがない身なのでなにを書こうかな...
と悩んでいたら初日の記事が弊学科のとある課題についてだったのでそれに習って、一年くらい前にやったカルマンフィルタの課題を引っ張り出してきました。
基本的には詳しい理論の方に突っ込まないように(深く理解しているとは言えないので)しているので理論的にガバガバなのはお許しください。また、個人的な備忘録として実装も載せていますが効率や可読性などは一切考えておりませんのでご容赦を・・・
そもそもカルマンフィルタってなに?
カルマンフィルタとは[1]によると
カルマンフィルター (Kalman filter) は、誤差のある観測値を用いて、ある動的システムの状態を推定あるいは制御するための、無限インパルス応答フィルターの一種である。
ということのようです。
これを読んで「ああ、なるほど」となる方はこれ以降の記事はあまり参考にならないかと思います。また、実装が知りたいという方もこの先しばらくは説明が続きますので読み飛ばしてくださって構いません。
さて、個人的な理解ではカルマンフィルタとは「ベイズの定理の応用によって数理モデルと観測値から精度よくシステムの状態推定を行うプログラム」と考えています。ポイントとなるのはベイズの定理、数理モデル、状態推定、と言ったところでしょうか?
ベイズの定理
ベイズの定理とは条件付き確率に関する定理です。最近ではベイズ主義統計学が一部で流行しているようなのでご存知の方は多いかも。
この定理の特徴は確率というものとして事前確率と事後確率というものを仮定しているところでしょう。事前・事後の「事」というのは、情報の入手を表しています。すなわち情報が入ってくる前と後で確率がどのように変化するかを記述した定理がベイズの定理です。数式で表すと
$$
\begin{equation}
P(B|A)=\frac{
P(A|B)
}{P(A)}\cdot P(B)
\end{equation}
$$
上の式の説明を少ししますとのように表される記号は|の右に書かれた事象が真であるときに、左側に書かれた事象も真である確率を表しています。そして、式の左辺の確率
を事後確率、式の右辺の
を事前確率と呼び事前確率から事後確率を求める方法を記しているということになります。
このベイズの定理を基礎に置いた統計学はベイズ主義統計と呼ばれるのですが、この統計学は高校で習うような頻度主義統計学とは大きく異なる特徴がいくつかあります。
まず、頻度主義統計学では確率的事象の裏にはなんらかの分布が存在していて、事象はその確率分布に従って発生するという思想のもとに発展しています。この思想のもとでは、仮にデータから分布を推定しようとした場合に無限点のサンプルが必要となってきます。
一方で、ベイズ主義統計学では最初に人間の主観的な尺度で分布を定めて置いてもサンプリングによってその分布の推定を修正していくことができます。ここで、分布を人間が主観的な尺度で定めると書いたのですが、やや暴論とも言えるこの仮定のためにベイズ主義統計と頻度主義統計はしばしば対立してきたそうです。一方でこの仮定によって少ないサンプリング数でも比較的精度よく推定を行うことができるため、あまり多くのサンプリングを行うことができない事例に対しても適用できるなど使い勝手がいい面も多くあります。
数理モデル
カルマンフィルタはとても強力な推定器ですが、取り扱うシステムのモデルが分かっているという前提があります。ここでいうモデルとは、状態遷移や観測の数学的表現、あるいはノイズの性質などが挙げられます。(通常の)カルマンフィルタの扱うことができるモデルにはいくつかの制約がかかっています。一つ一つ上げていきます。
システムは線形の動的システムであること
ノイズはゼロ平均のガウス分布に従い、他と無相関であること(白色ノイズであること)
初期状態の事前分布は(多変量)ガウス分布であること
フィルタ後の分布もガウス分布に従うこと
まず1.の制約について、カルマンフィルタは状態空間表現されたシステムを扱うといいかえてしまうことができます。それ以外の表現でも適用可能かもしれない・・・
このようなシステムは以下のような数学的表現ができます(離散時間系)
$$ \begin{cases} \mathbf{x}_{t+1}=\mathbf{A}\mathbf{x}_t+\mathbf{B}\mathbf{u}_t+\mathbf{w}_t \\ \mathbf{y}_{t} =\mathbf{C}\mathbf{x}_t+\mathbf{v}_t \end{cases} $$
なお、状態方程式や観測方程式に少し操作を加えることで非線形システムへの拡張が可能であり、これらには拡張カルマンフィルタ(Extended Kalman Filter, EKF)や無香カルマンフィルタ(Unscented Kalman Filter, UKF)などの種類があります。EKFはともかくとしてUKFはあまり実装も落ちていないようなので実装も上げておこうと思います。
2.の制約に関しては、
$$ \begin{align} \mathbf{w}_t\sim N(\mathbf{0},\mathbf{Q}) \\ \mathbf{v}_t\sim N(\mathbf{0}, \mathbf{R}) \end{align} $$
と表現できます。
3.4.の制約に関しては
$$ \begin{align} p(\mathbf{x}_1)&=N(\mathbf{x}_1|\mathbf{m}_0,\mathbf{V}_0) \\ p(\mathbf{x}_t|\mathbf{y}_{1:t})&=N(\mathbf{x}_t|\mathbf{m}_t,\mathbf{V}_t) \end{align} $$
となります。この表現からも分かる通り、カルマンフィルタではベイズの定理を用いて現在の状態の分布から次の状態の分布を推定することを行います。
状態推定
カルマンフィルタは上述したベイズの定理と数理モデルを用いて状態量の推定を行うプログラムです。実装という観点から見れば関数として表現できます。現在の状態を受け取って次の状態の推定値を出力する関数です。
個人的に重要だな、と思っている点として
ベイズの定理を用いることで事後確率分布の分散が事前確率分布の分散よりも減少すること
最初の事前確率分布は人間が恣意的に決めて良いということ
モデルが分かっている必要があること
が挙げられます。1点目に関しては証明の詳細は載せませんが、この性質によりカルマンフィルタによる推定が意味のあるものになります。
2点目に関しては、初期の状態量の共分散行列は自分で設定するものだ、ということを表しています。すなわち、初期状態の共分散行列はハイパーパラメータの一種であるということです。
また、3点目は当たり前なのですが、モデルが分かっていない系に関しては適用できないということです。この場合は別の手法を用いてノイズの性質を調べたり、物理モデリングによってモデルを推測するなどしてある程度信頼できるモデルを用意しておく必要があるということを意味しています。
まとめ
ここまでの話をまとめます。カルマンフィルタとは状態量の確率分布を推定するプログラムです。推定は2つのステップからなります。それぞれ、状態の遷移に伴う分布の更新(ここで事前分布を求めます)を行うステップと、観測情報によって事前分布を修正して事後分布を求めるステップです。この事後分布がそのステップにおける推定された分布ということになります。
カルマンフィルタはこれを繰り返すことにより、次々と状態を推定して刻々と変化する状況に対応するのです。
余談ですが、カルマンフィルタのカルマンはルドルフ・エミール・カルマンであり、カルマン渦のカルマン(フォンカルマン)とは別人のようです。どちらもハンガリー出身ということなのでハンガリーではメジャーな姓なのかもしれません。
アルゴリズム
定理の用意
アルゴリズムの詳細に入る前に多変量ガウス分布の定理に関して2つ定理の用意をします。これらはアルゴリズムの中で使われカルマンゲインの決定などに重要な役割を果たす定理です。
1.多変量ガウス分布の線形結合に関する定理
2.多変量ガウス分布の条件付き分布に関する定理
1.に関しては以下のように表現できます。
状態量とその線型結合で表されるベクトル
があり両者の間には
$$
\begin{equation}
\mathbf{y}=\mathbf{A}\mathbf{x}+\mathbf{b}+\mathbf{v}
\end{equation}
$$
なる関係が成り立つとします。、
であるとき
$$ \begin{equation} p(\mathbf{y})=N(\mathbf{y}|\mathbf{A}\mathbf{m}+\mathbf{b},\mathbf{A}\mathbf{P}\mathbf{A}^T+\mathbf{R}) \end{equation} $$
となるというものです。これにより線型結合結合で表された状態方程式や観測方程式を用いて状態量の確率分布の遷移を考えることができるようになります。
一方、2.に関しては以下のようなものです。ベクトルの同時確率密度分布が次式のような多変量ガウス分布に従うとします(縦棒が長くなってくれない・・・)。
$$
\begin{equation}
p(\mathbf{x},\mathbf{y})=N\left(\left[\begin{matrix}
\mathbf{x} \\
\mathbf{y}
\end{matrix}
\right]\mid \left[\begin{matrix}
\mathbf{a} \\
\mathbf{b}
\end{matrix}
\right], \left[\begin{matrix}
\mathbf{P} & \mathbf{R}\\
\mathbf{R}^T & \mathbf{Q}
\end{matrix}
\right]\right)
\end{equation}
$$
このとき、、
の周辺分布は
$$
\begin{align}
p(\mathbf{x})=N(\mathbf{x}|\mathbf{a}, \mathbf{P}) \\
p(\mathbf{y})=N(\mathbf{y}|\mathbf{b}, \mathbf{Q})
\end{align}
$$
となります。ここで一方の値が得られた時、もう一方の条件付き分布は、 $$ \begin{align} p(\mathbf{x}|\mathbf{y})=N(\mathbf{x}|\mathbf{a}+\mathbf{R}\mathbf{Q}^{-1}(\mathbf{y}-\mathbf{b}),\mathbf{P}-\mathbf{R}\mathbf{Q}^{-1}\mathbf{R}^T) \\ p(\mathbf{y}|\mathbf{x})=N(\mathbf{y}|\mathbf{b}+\mathbf{R}^T\mathbf{P}^{-1}(\mathbf{x}-\mathbf{a}),\mathbf{Q}-\mathbf{R}^T\mathbf{P}^{-1}\mathbf{R}) \end{align} $$
となります。この定理により、状態量の事前分布が分かっていて観測が得られたときに事後分布を求めることができるようになります。
さて、定理の用意ができたところでカルマンフィルタアルゴリズムの詳細に移って行きます。カルマンフィルタの目的はフィルタされた分布の再帰的な更新式、つまり入力と同じ形式の出力を得ることになります。数式を用いると
$$ \begin{align} p(\mathbf{x}_t|\mathbf{y}_{1:t})&=N(\mathbf{x}_t | \mathbf{m}_t, \mathbf{V}_t)\ \ (at\ Time\ t ) \\ p(\mathbf{x}_{t+1}|\mathbf{y}_{1:t+1}&)=N(\mathbf{x}_{t+1} | \mathbf{m}_{t+1}, \mathbf{V}_{t+1})\ \ (at\ Time\ t+1 ) \end{align} $$
のようなフィルタ分布を求めて行きます。すなわち、から
を求めることが目的です。
カルマンフィルタのアルゴリズムは二つのステップからなります。
- 次の時刻の状態をモデルを用いて予測する:
(時刻tにおいて)
2.次の時刻の観測に基づき推定を更新する:
一つずつ見て行きます。
予測ステップ
まず予測ステップですが、時刻におけるフィルタ分布を以下のように仮定します。
$$
\begin{equation}
p(\mathbf{x}_t|\mathbf{y}_{1:t})=N(\mathbf{x}_t|\mathbf{m}_t,\mathbf{V}_t)
\end{equation}
$$
ここで状態方程式は以下のように表されるのでした。 $$ \begin{cases} \mathbf{x}_{t+1}=\mathbf{A}\mathbf{x}_t+\mathbf{B}\mathbf{u}_t+\mathbf{w}_t \\ \mathbf{w}_t \sim N(\mathbf{0},\mathbf{Q}) \end{cases} $$
これに多変量ガウス分布の線形結合に関する定理を適用すると、1ステップ後の状態量の予測分布が計算されます。 $$ \begin{align} p(\mathbf{x}_{t+1}|\mathbf{y}_{1:t})&=N(\mathbf{x}_{t+1}|\mathbf{A}\mathbf{m}_t+\mathbf{B}\mathbf{u}_t, \mathbf{A}\mathbf{V}_t\mathbf{A}^T+\mathbf{Q}) \\ &=N(\mathbf{x}_{t+1}|\check{\mathbf{m}}_{t+1}, \check{\mathbf{V}}_{t+1}) \end{align} $$
ここでは予測分布に関する量を表すとします。
観測更新ステップ
続いて観測更新ステップについて説明します。
観測更新ステップにおいては前のステップにおいて計算した状態量の予測分布から状態量
と観測量
の予測同時分布
を計算します。この計算には多変量ガウス分布の線形結合に関する定理を用います。
その後得られた観測値を用いて多変量ガウス分布の条件付き確率に関する定理からフィルタ分布を求めます。これが目的としていた分布になります。
数式を用いて追って行きます。
観測方程式は
$$
\begin{cases}
\mathbf{y}_{t+1}=\mathbf{C}\mathbf{x}_{t+1}+\mathbf{v}_{t+1} \\
\mathbf{v}_{t+1}\sim N(\mathbf{0}, \mathbf{R})
\end{cases}
$$
これを状態量の予測分布に適用します。このとき
であったことより
$$
\begin{equation}
p(\mathbf{x}_{t+1}, \mathbf{y}_{t+1}|\mathbf{y}_{1:t})=N\left(\left[\begin{matrix}
\mathbf{x}_{t+1} \\
\mathbf{y}_{t+1}
\end{matrix}\right] \mid \left[\begin{matrix}
\check{\mathbf{m}}_{t+1} \\
\mathbf{C}\check{\mathbf{m}}_{t+1}
\end{matrix}\right], \left[\begin{matrix}
\check{\mathbf{V}}_{t+1} & \check{\mathbf{V}}_{t+1}\mathbf{C}^T \\
\mathbf{C}\check{\mathbf{V}}_{t+1} & \mathbf{C}\check{\mathbf{V}}_{t+1}\mathbf{C}^T+\mathbf{R}
\end{matrix}\right]
\right)
\end{equation}
$$
こうして得られた予測同時分布と実際の観測値を用いてフィルタ分布は以下のように求められます。
$$ \begin{align} p(\mathbf{x}_{t+1}|\mathbf{y}_{t+1}, \mathbf{y}_{1:t})&=p(\mathbf{x}_{t+1}|\mathbf{y}_{1:t+1}) \\ &=N(\mathbf{x}_{t+1}|\check{\mathbf{m}_{t+1}}+\mathbf{K}_{t+1}(\mathbf{y}_{t+1}-\mathbf{C}\check{\mathbf{m}}_{t+1}),(\mathbf{I}-\mathbf{K}_{t+1}\mathbf{C})\check{V}_{t+1}) \\ \mathbf{K}_{t+1}&=\check{\mathbf{V}}_{t+1}\mathbf{C}^T(\mathbf{C}\check{\mathbf{V}}_{t+1}\mathbf{C}^T+\mathbf{R})^{-1} \end{align} $$
ここで出てきたはカルマンゲインと呼ばれ、観測値と予測値のどちらをより信頼するかという重みのようなものになります。
まとめ
これでカルマンフィルタアルゴリズムはおしまいです。あとは繰り返してステップを更新していくだけです。
実装
これまでの流れをひとまずPythonで実装して見ました。ちなみに弊学科の標準語はPythonです。for文が遅いとか色々ありますが僕は好きです。
問題設定
XY平面上で]に原点を出発し、45度方向に秒速
]で移動している物体があるとします。この移動には外乱による影響があるとします。また、1秒ごとに位置座標の観測があるとします。この観測にもノイズが含まれているとします。この物体の位置をカルマンフィルタを用いて推定して見ます。
学科の人が見たら、これは・・・となってしまいそうな問題設定ですが気にしないで行きます。
系の設定
さて、全てをシミュレーションで行うとなると真値系と推定系を設定しなければなりません。真値系は真値を計算しつつ誤差の乗った観測値を吐き出します。推定系は誤差の乗った観測を受け取りながら推定値を計算し続けます。まずは真値系から。
なおモデルの更新式に関しては、カルマンフィルタのものと同一なので関数化します。
import numpy as np import numpy.random as random import matplotlib.pyplot as plt # 関数 def model(x, A, B, u): v = 2.0 return np.dot(A, x) + B * v def true(x): noise = random.normal(0.0, 1.0, (2, 1)) return x + noise def system(x): true_val = true(model(x)) obs_val = true(true_val) return true_val, obs_val
続いて推定系を検討します。カルマンフィルタは実装としては関数で表現できます。
def Kalman_Filter(m, V, y, A, B, u, Q, R): # 予測 m_est = model(x, A, B, u) V_est = np.dot(np.dot(A, V), A.transpose()) + Q # 観測更新 K = np.dot(V_est, np.linalg.inv(V_est + R)) m_next = m_est + np.dot(K, (y - m_est)) V_next = np.dot((np.identity(2) - K), V_est) return m_next, V_next
最後に状態量などを定義して与えてやります。
if __name__ == "__main__": A = np.identity(2) # 状態方程式のA B = np.ones((2, 1)) # 状態方程式のB u = 2.0 # 速度 x = np.zeros((2, 1)) # 真値 m = np.zeros((2, 1)) # 推定値 V = np.identity(2) # 推定値の初期共分散行列(勝手に設定して良い) Q = 2 * np.identity(2) # 入力誤差の共分散行列(今回はtrue()の中でnoiseの分散を2.0に設定したので) R = 2 * np.identity(2) # 上と同じ # 記録用 rec = np.empty((4, 30)) # main loop for i in range(30): x, y = system(x, A, B, u) m, V = Kalman_Filter(m, V, y, A, B, u, Q, R) rec[0, i] = x[0] rec[1, i] = x[1] rec[2, i] = m[0] rec[3, i] = m[1] # 描画 plt.plot(rec[0, :], rec[1, :], color="blue", marker="o", label="true") plt.plot(rec[2, :], rec[3, :], color="red", marker="^", label="estimated") plt.legend() plt.show()
この結果は以下の図のようになります。
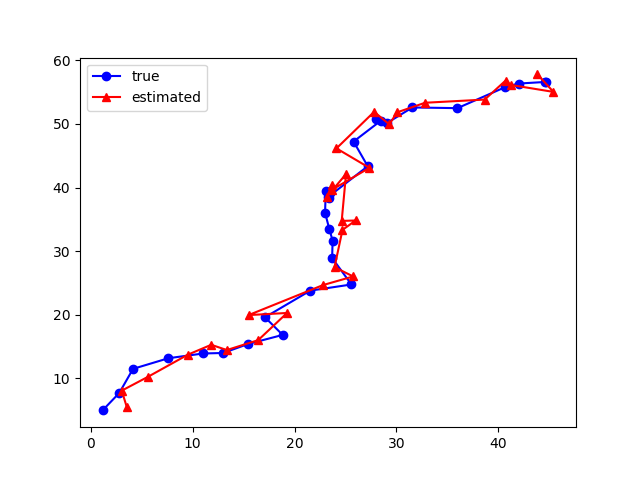
グラフがかなりうねっていますが追従できているのがわかります。
なお、上の実装では観測方程式がない(状態がそのまま観測になる)ようになっているのでご注意ください。観測方程式がある場合は観測更新ステップが
K = np.dot(V_est, np.dot(C.transpose(), np.linalg.inv(np.dot(C, np.dot(V_est, C.transpose())) + R)))
m_next = m_est + np.dot(K, (y - np.dot(C, m_est)))
V_next = np.dot((np.identity(2) - np.dot(K, C)), V_est)
となります。ドット積をnp.dotで書かなければならないのがnumpyの悪いところですね・・・。Python3系では@演算子でドット積を表現できるようなので後方互換性を気にしないならその方がいいでしょう。
拡張カルマンフィルタ
カルマンフィルタを非線形システムを扱えるように拡張したのが拡張カルマンフィルタです。EKFとか呼ばれます。
拡張はとても簡単で状態方程式のや観測方程式の
を非線形関数のヤコビアンに変えるだけです。
数式で表すと、
$$
\begin{align}
\mathbf{x}_{t+1}&=f(\mathbf{x}_t, \mathbf{u}_t) + \mathbf{w}_t \\
\mathbf{y}_t &= h(\mathbf{x}_t)+\mathbf{v}_t \\
\mathbf{A}_t&=\frac{\partial f(\mathbf{x}, \mathbf{u})}{\partial \mathbf{x}}\mid_{\mathbf{x}=\mathbf{m}_t, \mathbf{u}_t} \\
\mathbf{C}_t&=\frac{\partial h(\mathbf{x})}{\partial \mathbf{x}}\mid_{\mathbf{x}=\check{\mathbf{m}}_{t+1}}
\end{align}
$$
EKFの例題
EKFを使った推定を行って見ます。
2次元平面を等速円運動「しようと」している物体があるとします。この物体には外乱が加わっているとします。
原点にいる観測者からは、各時刻で、物体への距離と方位角が計測できるとします。この観測には観測ノイズが加わります。
円運動の半径は]とし、角速度は
、物体位置に対するノイズの分散は
、物体への距離の観測のノイズの分散は
、物体の方位角の分散は
とします。
実装
線形問題の時と同様にしてまずは真値系の実装をします。
状態方程式は $$ \begin{equation} \left[ \begin{matrix} x_{1, t} \\ x_{2, t} \end{matrix}\right] = \left[\begin{matrix} x_{1, t-1} \\ x_{2, t-1} \end{matrix}\right] + \left[\begin{matrix} -L\omega\sin\omega t \\ L\omega\cos\omega t \end{matrix}\right] + \mathbf{w}_t \end{equation} $$ また、観測方程式は $$ \begin{equation} \left[\begin{matrix} y_{1, t} \\ y_{2, t} \end{matrix}\right] = \left[\begin{matrix} \sqrt{x^2_{1, t}+x^2_{2, t}} \\ \tan^{-1}\frac{x_{2,t}}{x_{1, t}} \end{matrix}\right] + \mathbf{v}_t \end{equation} $$
です。
import numpy as np import numpy.random as random import matplotlib.pyplot as plt # 関数 def state_eq(x, L, omega, t): x_new = x + np.array([-L*omega*np.sin(omega*t), L*omega*np.cos(omega*t)]).reshape([2, 1]) return x_new def obs_eq(x, obs_noise_y1, obs_noise_y2): x1 = x[0] x2 = x[1] y = np.array([np.sqrt(x1**2 + x2**2), np.arctan(x2/x1)]).reshape([2, 1]) noise = np.array([random.normal(0, obs_noise_y1), random.normal(0, obs_noise_y2)]).reshape([2, 1]) return y + noise def obs_eq_noiseless(x): x1 = x[0] x2 = x[1] y = np.array([np.sqrt(x1**2 + x2**2), np.arctan(x2/x1)]).reshape([2, 1]) return y def true(x, input_noise): noise = random.normal(0, input_noise, (2, 1)) return x + noise
冗長なコードが見えていますが、目を瞑ってください。
続いて推定系。推定系では状態方程式のヤコビアンが必要になってきます。
ヤコビアンは、状態方程式に関しては $$ \begin{equation} \frac{\partial f(\mathbf{x}, \mathbf{u})}{\partial \mathbf{x}}\mid_{\mathbf{x}=\mathbf{m}_t, \mathbf{u}_t}= \left[ \begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}\right] \end{equation} $$
観測方程式に関しては、 $$ \begin{equation} \frac{\partial h(\mathbf{x})}{\partial \mathbf{x}}\mid_{\mathbf{x}=\check{\mathbf{m}}_{t+1}}= \left[ \begin{matrix} \frac{ x_{1,t} }{ \sqrt{ x^2_{1,t} + x^2_{2,t} } } & \frac{ x_{2,t} }{ \sqrt{ x^2_{1,t} + x^2_{2,t} } } \\ -\frac{ x_{2,t} }{ x^2_{1,t} + x^2_{2,t} } & \frac{ x_{1,t} }{ x^2_{1,t} + x^2_{2,t} } \end{matrix} \right] \end{equation} $$
これとEKFの実装をすると
def state_jacobian(): jacobian = np.identity(2) return jacobian def obs_jacobian(x): jacobian = np.empty((2, 2)) jacobian[0][0] = x[0] / np.sqrt(x[0]**2 + x[1]**2) jacobian[0][1] = x[1] / np.sqrt(x[0]**2 + x[1]**2) jacobian[1][0] = -x[1] / (x[0]**2 + x[1]**2) jacobian[1][1] = x[0] / (x[0]**2 + x[1]**2) return jacobian def system(x, L, omega, t, input_noise, obs_noise_y1, obs_noise_y2): true_state = true(state_eq(x, L, omega, t), input_noise) obs = obs_eq(true_state, obs_noise_y1, obs_noise_y2) return true_state, obs def EKF(m, V, y, Q, R, L, omega, t): # 予測ステップ m_est = state_eq(m, L, omega, t) A = state_jacobian() V_est = np.dot(np.dot(A, V), A.transpose()) + Q # 観測更新ステップ C = obs_jacobian(m_est) temp = np.dot(np.dot(C, V_est), C.transpose()) + R K = np.dot(np.dot(V_est, C.transpose()), np.linalg.inv(temp)) m_next = m_est + np.dot(K,(y - obs_eq_noiseless(m_est))) V_next = np.dot(np.identity(V_est.shape[0]) - np.dot(K, C), V_est) return m_next, V_next
最後に状態量などの設定を行って完了です。
if __name__ == "__main__": x = np.array([100, 0]).reshape([2, 1]) L = 100 omega = np.pi / 10 input_noise = 1.0**2 obs_noise_y1 = 10.0**2 obs_noise_y2 = (5.0 * np.pi / 180)**2 m = np.array([100, 0]).reshape([2, 1]) t = 0.0 dt = 1.0 V = np.identity(2) * 1.0**2 Q = np.identity(2) * input_noise R = np.array([[obs_noise_y1, 0], [0, obs_noise_y2]]) # 記録用 rec = np.empty([4, 21]) for i in range(21): rec[0, i] = x[0] rec[1, i] = x[1] rec[2, i] = m[0] rec[3, i] = m[1] x, y = system(x, L, omega, t, input_noise, obs_noise_y1, obs_noise_y2) m, V = EKF(m, V, y, Q, R, L, omega, t) t += dt plt.plot(rec[0, :], rec[1, :], color="blue", marker="o", label="true") plt.plot(rec[2, :], rec[3, :], color="red", marker="^", label="estimated") plt.legend() plt.show()
この結果は以下の図のようになります。
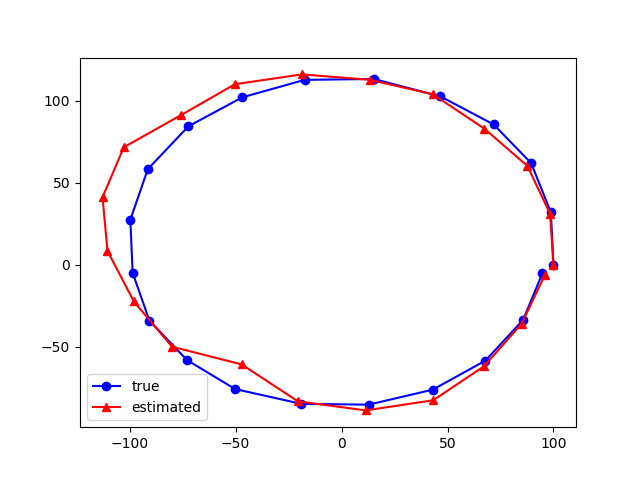
ノイズの元でも比較的正確に推定ができていそうです。
無香カルマンフィルタ
最後に紹介するのが、EKFと同じく非線形に拡張されたカルマンフィルタである、無香カルマンフィルタ(Unscented Kalman Filter, UKF)です。
UKFではヤコビアンを計算してガウス分布の線形結合による変化を考察する代わりに、シグマ点と呼ばれる代表点をガウス分布から抽出し、その点群を状態方程式や観測方程式を直接通すことによってガウス分布の変形を検討します。
具体的な理論に関しては、割愛させていただきますが、[2]などに詳しく載っています。
卒論で使ったので実装の備忘録としてこちらに載せさせていただきます。
# UKF Parameters ukf_lambda = 10.0 # UKFのλパラメータ ukf_kappa = 0.1 # UKFのκパラメータ ukf_alpha2 = (2.0 + ukf_lambda)/(2.0 + ukf_kappa) # UKFのα^2パラメータ ukf_w0_m = ukf_lambda/(2.0 + ukf_lambda) # UKFの重みパラメータ ukf_w0_c = ukf_w0_m + (1.0 - ukf_alpha2 + 2.0) # UKFの重みパラメータ ukf_wi = 1.0/(2.0*(2.0 + ukf_lambda)) # UKFの重みパラメータ ukf_wm = np.zeros([5, 1]) # UKFの重みパラメータw_m ukf_wc = np.zeros([5, 1]) # UKFの重みパラメータw_c ukf_gamma = np.sqrt(3.0 + ukf_lambda) # γ = √(n + λ) # UKFの重みパラメータの設定 ukf_wm[0] = ukf_w0_m ukf_wc[0] = ukf_w0_c for i in range(1, 5): ukf_wm[i] = ukf_wi ukf_wc[i] = ukf_wi def gen_sigma_point(mu, sigma): """ Function to generate Matrix chi which is the set of the sigma point Vector. arguments : mu : Vector of the mean values. sigma : Correlation Matrix. return : chi : Matrix chi. """ n = len(mu) # 次元 chi = np.zeros([n, 2*n+1]) # χ行列 root_sigma = np.linalg.cholesky(sigma) # √Σの計算 chi[:, 0] = mu[:, 0] chi[:, 1:1+n] = mu + ukf_gamma*root_sigma chi[:, 1+n:2*n+1] = mu - ukf_gamma*root_sigma return chi def gen_correlation_mat(mu, chi, R): """ Function to describe the change of the correlation matrix. arguments : mu : Vector of the mean values. chi : Destribution of the sigma point. R : Correlation Matrix of the observation noise. return : sigma_bar : Correlation Matrix after the change. """ sigma_bar = R for i in range(chi.shape[1]): x = chi[:, i].reshape((chi.shape[0], 1)) - mu sigma_bar = sigma_bar + ukf_wc[i]*(np.dot(x, x.T)) return sigma_bar def UKF(mu, sigma, u, z, state_func, obs_func, R, Q, dt): """ Unscented Kalman Filter Program. arguments : mu : Vector which is the set of state values. sigma : Correlation Matrix of the state values. u : Control inputs.Vector/Float. z : Observed values. state_func : Function which describe how the state changes. obs_func : Function to get observed values from state values. R : Correlation Matrix of the noise of the state change. Q : Correlation Matrix of the observation noise. dt : Time span of the integration. returns : mu : Vector which is the set of state values. sigma : Correlation Matrix of the state values. --------------- """ # Σ点生成 chi = gen_sigma_point(mu, sigma) # χ # Σ点の遷移 chi_star = state_func(u, chi, dt) # 事前分布取得 mu_bar = np.dot(chi_star, ukf_wm) # 平均の事前分布 sigma_bar = gen_correlation_mat(mu_bar, chi_star, R) # 共分散行列の事前分布 # Σ点の事前分布 chi_bar = gen_sigma_point(mu_bar, sigma_bar) # 観測の予測分布 z_bar = obs_func(chi_bar) # 観測の予測値 z_hat = np.dot(z_bar, ukf_wm) # 観測の予測共分散行列 S = gen_correlation_mat(z_hat, z_bar, Q) # Σ_xzの計算 sigma_xz = np.zeros([mu.shape[0], z.shape[0]]) for i in range(chi_bar.shape[1]): x_ = chi_bar[:, i] - mu_bar[:, 0] z_ = z_bar[:, i] - z_hat[:, 0] x_ = x_.reshape((x_.shape[0], 1)) z_ = z_.reshape((z_.shape[0], 1)) sigma_xz = sigma_xz + ukf_wc[i]*(np.dot(x_, z_.T)) # カルマンゲインの計算 K = np.dot(sigma_xz, np.linalg.inv(S)) # 戻り値の計算 mu = mu_bar + np.dot(K, (z - z_hat)) sigma = sigma_bar - np.dot(np.dot(K, S), K.T) return mu, sigma
実際に使う際には問題に合わせてシグマ点の遷移を記述する関数の用意が必要です。
今回は先ほどのEKFの例をUKFでも推定して見ましょう。状態方程式と観測方程式を記述した関数を用意します。
def state_func(u, chi, dt): L = 100 omega = np.pi / 10 return chi + np.array([[-L*omega*np.sin(omega*u)], [L*omega*np.cos(omega*u)]]) def obs_func(chi_bar): obs = np.zeros_like(chi_bar) for i in range(chi_bar.shape[1]): obs[0][i] = np.sqrt(chi_bar[0, i]**2+chi_bar[1, i]**2) obs[1][i] = np.arctan(chi_bar[1, i] / chi_bar[0, i]) return obs
これを用いて推定をしてみると・・・
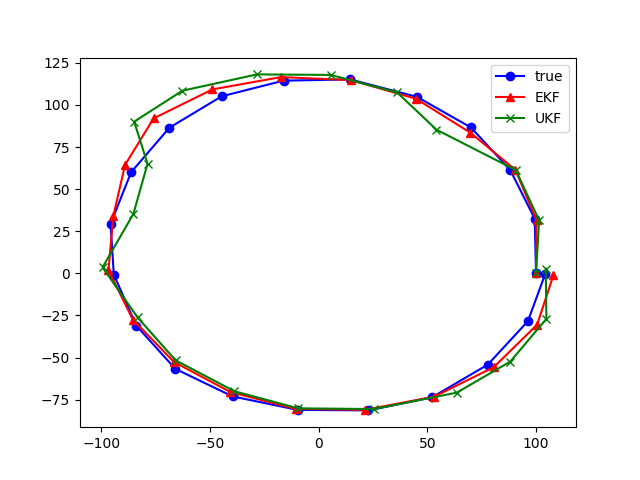
このようになります。この例ではEKFの方が性能が良さそうですね・・・。
実際にところ、UKFによる推定はEKFより計算量が多いものの精度は高くなることが多いようです。
一方で、ノイズが強かったりすると共分散行列が正定値行列ではなくなってコレスキー分解ができなくなり推定が止まってしまうようなことも起きます。
今回の問題設定では、状態方程式や観測方程式があまり性質の良いものではなく、ノイズも強いためあまり推定がうまくいっていないようです。
出典
[1] Wikipedia. カルマンフィルター. Retrieved December 7, 2017, from, https://ja.wikipedia.org/wiki/カルマンフィルター [2]確率ロボティクス. Sebastian Thrun, Wolfram Burgard, Dieter Fox. 上田隆一訳. マイナビ出版, 2015. ISBN 4839952981, 9784839952983